今年的數學考試大綱發布啦，相較于2019年大綱，今年有什么變動呢?大家一定要密切關注。

2020年考研數學大綱已經呈現在我們的眼前，相較于2019年大綱，考研數學數一、數二、數三-高數、線代、概率論所有科目加到一起的變化數為0。

試卷內容結構上，毫無變化。數學一、數學三:高等數學、線性代數、概率論與數理統計分別占比依舊為56%、22%、22%，數學二:高等數學、線性代數分別占比78%、22%。

試卷題型結構上，永遠的“869”。分別是8道選擇、6道填空、9道解答，共23題。選擇每題4分，共32分;填空每題4分，共24分;解答題共94分。經過詳細比對我們發現每個科目的考點和相應的考試要求都與去年并無二致。

可以說，2020年考研數學大綱就是2019年的大綱換了個“帽子”。不僅如此，2010-2019總共十年的時間里，考研數學大綱也只有一處變化，而這一處變化也只是知識點名稱的變化。所以，縱觀以往，考研數學不過是個“新古董”而已。而這個“新古董”就是我們考研復習唯一的官方文件，也就是考研命題的依據和出發點，我們的復習都應圍繞著它來展開。

函數、極 限、連續

考試內容

函數的概念及表示法、 函數的有界性、單調性、周期性和奇偶性 復合函數、反函數、分段函數和隱函數 基本初等函數的性質及其圖形 初等函數 函數關系的建立

數列極 限與函數極 限的定義及其性質 函數的左極 限與右極 限 無窮小量和無窮大量的概念及其關系 無窮小量的性質及無窮小量的比較 極 限的四則運算 極 限存在的兩個準則：單調有界準則和夾逼準則 兩個重要極 限：

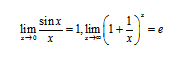
函數連續的概念 函數間斷點的類型 初等函數的連續性 閉區間上連續函數的性質

考試要求

理解函數的概念，掌握函數的表示法，并會建立應用問題的函數關系.

了解函數的有界性、單調性、周期性和奇偶性.

理解復合函數及分段函數的概念，了解反函數及隱函數的概念.

掌握基本初等函數的性質及其圖形，了解初等函數的概念.

5.理解極 限的概念，理解函數左極 限與右極 限的概念以及函數極 限存在與左極 限、右極 限之間的關系.

6.掌握極 限的性質及四則運算法則.

7.掌握極 限存在的兩個準則，并會利用它們求極 限，掌握利用兩個重要極 限求極 限的方法.

8.理解無窮小量、無窮大量的概念，掌握無窮小量的比較方法，會用等價無窮小量求極 限.

9.理解函數連續性的概念(含左連續與右連續)，會判別函數間斷點的類型.

10.了解連續函數的性質和初等函數的連續性，理解閉區間上連續函數的性質(有界性、最大值和最小值定理、介值定理)，并會應用這些性質.